PERCENTILE.EXC Function Excel – Usage and Example

The PERCENTILE.EXC Function in Excel came into existence in 2010. It is one of the essential Statistical functions.

So let’s begin learning the fundamentals of the PERCENTILE.EXC function.

When to Use PERCENTILE.EXC Function in Excel

The PERCENTILE.EXC word represents Percentile Exclusive. The PERCENTILE.EXC Function calculates the percentiles for an array of numerical values. The function has the ability to calculate the k^th percentile. The value of k can lie between 0 and 1.

The function is exclusive because all the values between 0 and 1 are not considered valid. The PERCENTILE.EXE function excludes the percentiles from 0 to 1/(N+1) as well as N/(N+1) to 1. Here N is the size of data.

Use the PERCENTILE.INC Function for k inclusive 0 to 1.

Syntax and Arguments

=PERCENTILE.EXC(array,k)

The following points explain the required function arguments for PERCENTILE.EXC Formula.

• array – This is the range of cells containing data. We can also pass the data set directly as the numbers within brackets separated by a comma.
• k- This is the percentile that we want to calculate. The value of k lies between 0 and 1. It can also be written in percentage form. k cannot be from 0 to 1/(N+1) as well as N/(N+1) to 1.

Here N is the number of items in our data set.

Excluded Range for k

This can be understood with a simple example. Let us suppose the data has 6 items ( N=6 ). Then the value of k cannot be:-

• from 0 to 1/(N+1)

0 to 1/(6+1)

0 to 0.42

• and the value of k cannot be:-

from N/(N+1) to 1

6/(6+1) to 1

0.85 to 1

So here we come to the result that if our data has 6 items, then we cannot calculate the percentiles from 0% to 42% and 85% to 100% using PERCENTILE.EXC function.

What does the k^th Percentile Indicate?

Let us suppose we want to get the value of the 60 percentile for the above data. The 60th percentile for this data is 5.

Conclusion – The value 5 indicates that 60% of the entire data have values either less than or equal to 5.

If the kth percentile result is x, then k% values in data are either less than or equal to x, where the value of k cannot be from 0 to 1/(N+1) and N/(N+1) to 1. N is the total number of items in data set,

Example to Implement PERCENTILE.EXC Formula in Excel

In this section of the blog, we would find percentile values for different percentages by using the PERCENTILE.EXC Formula.

We are given the following array of values in range A2:B12.

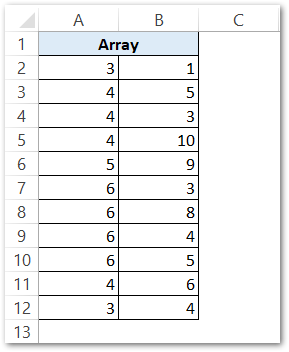
Step 1 – Find the excluded range of k

To avoid errors, we will first find the invalid values of k and then make sure to not use those values in the formula.

The value of k can be from 0 to 1 excluding two ranges.

0 to 1/(N+1) and N/(N+1) to 1, N is the number count.

We can count the total number of cells containing numerical values with the COUNT Formula.

=COUNT(A2:B12)

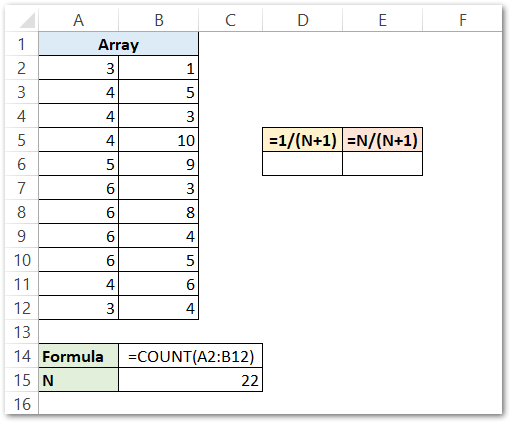
N = 22. We will replace the value of N with cell B15 containing the COUNT Function result.

Now use the following formulas in cells D6 and E6 respectively.

=1/(B15+1)

=B15/(B15+1)

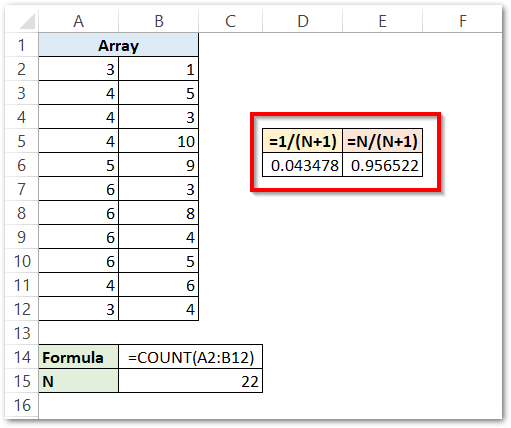
Consequently, we find that the value of k excludes the range 0 to 0.04 and 0.95 to 1.

However, the valid range of k begins from 0.043 to 0.955.

The excluded values of k depend on N. If we take an invalid value of k in our PERCENTILE.EXC formula, it returns a #NUM! error.

Step 2 – Finding the Percentile Value

As calculated, the percentile value from 0% to 4.3 % and from 95.6% to 100% would be invalid.

We would like to find the following percentile values.

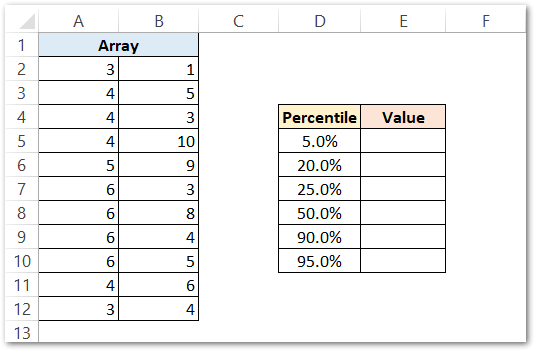
You can see that these percentiles in the range D5:D10 lie in the valid range of k.

Now use the following PERCENTILE.EXC Formula in cell E5.

=PERCENTILE.EXC($A$2:$B$12,D5)

Select the range E5:E10 and press the ctrl D key to copy the formula down.

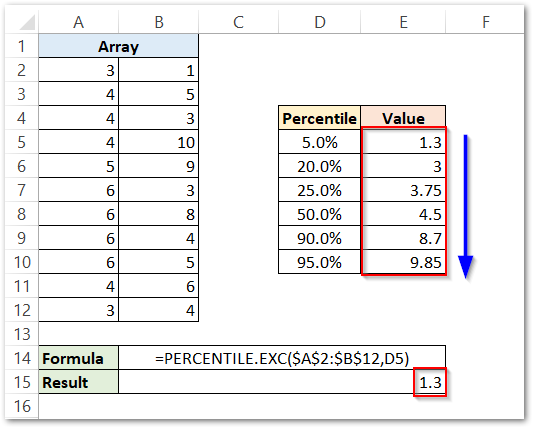
As a result, the formula returns the value of the 5^th, 20^th, 25^th, 50^th, 90^th and 95^th percentile as 1.3, 3, 3.75, 4.5, 8.7 and 9.85 respectively.

Explanation – We have passed the range A2:B15 as the array argument of PERCENTILE.EXC Function. The array is locked using the $ sign ($A$2:$B$12) so that it does not change when we copy the formula for getting the remaining percentile values.

We supply the k argument as D5 for getting the value of the 5th percentile. Consequently, we get the fifth percentile as 1.3

This implies that 5% of the values are equal to or less than 1.3

Here we have come to the end of PERCENTILE.EXC Function blog,

Thank you for reading.