Previously, we implemented the CHISQ.DIST Function. In this blog, we will learn another important function that is closely related is CHISQ.INV Function in Excel.
So let us begin.
When to Use CHISQ.INV Function in Excel?
The CHISQ.INV Function calculates the inverse of Left Tailed Probability of Chi Square Distribution. It calculates the result based on the specified value of cumulative probability and degree of freedom.
CHISQ.INV can be categorized under the Statistical Functions of Excel. It came into existence in Excel 2010 and cannot be used in earlier versions of Excel.

Syntax and Arguments
=CHISQ.INV(probability,deg_freedom)
The information regarding the inputs required by CHISQ.INV Function is stated below.
- probability – This is the specified value of left tailed probability or cumulative probability of the Probability Density Function. Its value must lie in the interval [0,1] because it is probability.
- deg_freedom – This specifies the degree of freedom for Chi Square Distribution. It is an integral value lying between 1 and 1010.
Important Points Regarding CHISQ.INV Function
Before we start implementing the formula, here we have some important notes about CHISQ.INV Function in Excel.
- CHISQ.INV Function is an updated version of CHINV Function. If you have excel 2007 or an earlier version of excel, then you would use CHINV Function.
- The function truncates the value after the decimal point for a nonintegral value of the deg_freedom argument.
- The CHISQ.INV function returns a #VALUE! error for any non-numerical value supplied as any of the function’s input.
- We would encounter a #NUM! the error probably when:
- The value of the probability argument is less than zero or greater than 1.
- The deg_freedom argument does not lie in the interval [1,1010]
Example to Learn CHISQ.INV Function
Here, we would plot a graph for Chi Squared Distribution when degrees of freedom = 3 by using the CHI.DIST Function ( cumulative=FALSE ) .
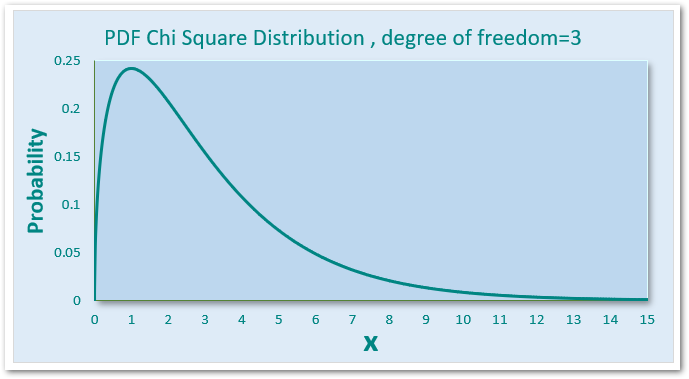
We would now find the inverse of the left tailed probability of Chi Square distribution when degree of freedom = 3 and left tailed probability = 0.738
=CHISQ.INV(0.738,3)
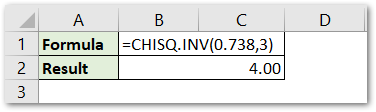
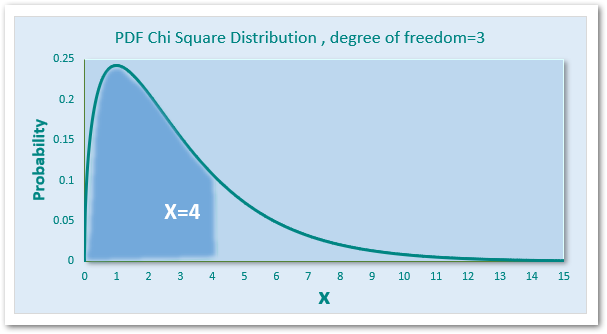
As a result, we get the value of x as 4.
Explanation – We have supplied the probability and deg_freedom argument as 0.738 and 3 respectively. The function calculates the value of x for the specified arguments. This is represented through the shaded area under the curve in the graph of the Probability Density function of Chi-Square Distribution.
This brings us to the end of the blog.
Thank you for reading.
