BINOM.DIST function in Excel – Probability of N Successes

The BINOM.DIST function in Excel is an essential Statistical Function that came into existence in 2010. The function is easy to understand in this first go.

So let us begin learning.

When to Use BINOM.DIST Function in Excel?

The word BINOM.DIST represents binomial distribution. The BINOM.DIST Function in Excel is used to get the probability of a number of successes when the same experiment is conducted several times. The BINOM.DIST Function has further two kinds of results:-

• Probability Distribution – this gets us the probability of exactly x number of successes in n number of trials,
• Cumulative Distribution – we would get the probability of having at most x number of successes in n number of trials

What does the Result of BINOM.DIST Function Implies Calculates?

This can be understood with a simple example. Let us suppose tossing a coin is an experiment. Getting a head on the top of each coin is a success. We would repeat this experiment of tossing a coin 3 times. So the total number of trials n=3.

The following can be the possibilities when a coin is tossed three times:-

Coin 1	Coin 2	Coin 3	Number of Heads
Head	Head	Head	3
Head	Head	Tail	2
Head	Tail	Head	2
Tail	Head	Head	2
Head	Tail	Tail	1
Tail	Head	Tail	1
Tail	Tail	Head	1
Tail	Tail	Tail	0

There can be 8 possible outcomes when a coin is tossed 3 times

Probability Distribution

Let us suppose that getting a head on the coin is a success. The probability of getting a head on a coin is 1/2 and not getting a head is also 1/2 (tail on top). Therefore the probability of success is 1/2.

We want to get the probability of getting 2 heads when a coin is tossed three times. Here are three cases when we get two heads after tossing three coins.

(HHT,HTH,THH)

So the probability of getting exactly two heads when a coin is tossed three times would be 3/8

This is when we use the probability function of getting x number of successes when an experiment is conducted n times

Cumulative Distribution

There can be another situation when we want the probability of almost 2 heads ( 0 heads + 1 head + 2 heads )coming when the coin is tossed 3 times. The following would be favorable outcomes.

(TTT,HTT,THT,TTH,HHT,HTH,THH)

Therefore the probability of getting at most 2 heads when a coin is tossed 3 times in 7/8

This is when we use Cumulative Distribution to get the probability of at most x successes when the experiment is conducted n times.

Syntax and Examples

=BINOM.DIST(number_s,trials,probability_s,cumulative)

The following points contain important notes about BINOM.DIST Function in Excel.

• number_s – This function asks for the number of successes out of n trials. It cannot be a negative value or a value greater than the actual number of trials performed ( you can’t get 4 heads when a coin is tossed three times )
• trials – This is the number of times, the experiment is repeated ( rolling a dice 5 times, picking a card 10 times )
• probability_s – This is the probability of success in an experiment ( if getting 6 on dice is a success then the probability of getting a 6 when a die is rolled is 1/6 )
• cumulative – This argument is boolean and asks for the type of distribution. It can have two values.
  • FALSE – We want to get the probability of exactly x successes.
  • TRUE – We want the probability of at most x successes.

Examples to learn BINOM.DIST Function in Excel

In this section of the blog, we would be performing some experimentation with the BINOM.DIST Function.

Example 1 – Getting x Heads on Coin Tossed N Times

Let us suppose you have a coin and you tossed it once. There can be a head or a tail when on top of a coin upon tossing it. If Getting a Head on the coin is a success then the probability of success would be 1/2 or 0.50 or 50%.

If the same coin is tossed five times, then we want to find the probability of getting the head 2 times. Use the following BINOM.DIST function formula.

=BINOM.DIST(2,5,0.5,FALSE)

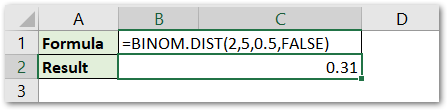
As a result, we get the probability of getting 2 heads when the coin is tossed 5 times to be 0.31 or 31%.

Explanation – The number of trials is 5 and the successes for which we want to find the probability is 3. So the number_s is 3 and trials argument is 5. Thereafter, the probability_s of getting success (head ) is 1/2 as each time the experiment is conducted ( coin is tossed ). At last, we set the cumulative argument as FALSE, as we want the result for exactly 2 heads.

If you want to get the probability of getting at most two heads, then you can keep the formula the same, just change the cumulative argument to TRUE.

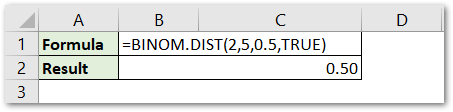
This implies that the probability of getting at most 2 heads ( zero head or 1 head or 2 heads ) when the coin is tossed five times is 0.50 or 50%.

Example 2 – Success in Throwing a Dice

Let us suppose a man has a dice. He assumes that getting a 1 or 6 on the dice is a success when he rolls the dice. The probability of getting success is 2/6.

The man rolls the dice 10 times. We want to know his chances of getting success 7 times ( getting a 1 or 6 seven times ).

We would use the following BINOM.DIST Function Formula.

=BINOM.DIST(7,10,2/6,FALSE)

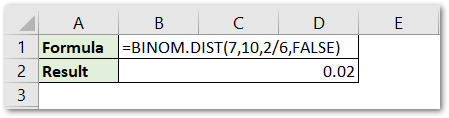
As a result, we know that his probability of getting a 1 or 6, seven times would be 0.02 or 2 %.

Explanation – We supplied the number_s and trials argument as 7 and 10 respectively. Success is defined by getting a 1 or 6 on the dice. Therefore, the probability_s argument is 2/6.

Similarly, we can find the chances of the man getting a one or six on dice at most 7 times, only by changing the cumulative argument to TRUE

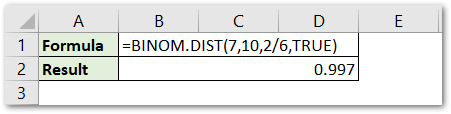
This implies. that the chances of getting a one or six, more than 7 times is only 0.003 or 0.3 %

You can use the BINOM.DIST.RANGE Function for the number of successes lying in a range.

This brings us to the end of the blog.

Thank you for reading.