In the earlier articles, we learned to find the Sin and Cosine of the angles using the functions in Excel. In this blog, we would implement another important Mathematical Function – TAN Function in Excel. So let us begin the fundamentals for implementing the formula.
When to Use TAN Function in Excel?
The word TAN represents Tangent. The TAN Function calculates the value of trigonometric ratio – Tangent for a particular angle in radians. In a right-angled triangle, tangent refers to the ratio of the Adjacent side to the opposite side against the angle θ.
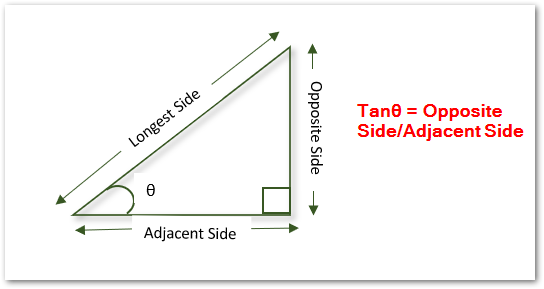
The ratio of the opposite side to the side adjacent to the angle θ is the trigonometric ratio Tangent for that angle.
The TAN Function in excel can calculate the value of this ratio for the angle θ in radians in a few clicks.
Also Read: COS Function in Excel – Usage with Examples
Graph of Tangent of Angle
The graph of the Tangent is as follows:
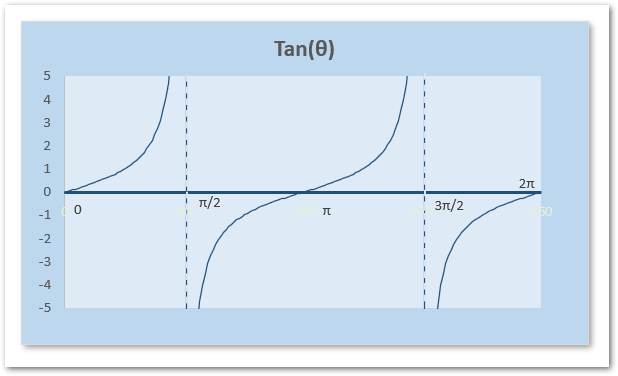
The graph of the tangent function shown above goes from zero to a full rotation of 360 degrees represented as 2π. The value of the tangent function is infinity for the angle closer to π/2 and 3π/2. These are two vertical asymptotes in the graph of Tanθ for 90° and 270°.
Syntax and Arguments
=TAN(number)
The TAN Function requires only one input parameter for its working,
- number – This is the angle in radians for which we want to get the value of the Tangent Function.
Important Points to Note about TAN Function
There are some important things to remember about the TAN function before we start implementing the formula.
- The TAN Function was introduced in Excel 2007 and cannot be used in earlier functions.
- The result of the TAN Function for an angle θ can also be obtained by the ratio of Sinθ and Cosθ
- We can convert an angle from degrees into radians using the PI Function or RADIANS Function in excel.

Examples to Learn TAN Function
In this section of the blog, we would execute the TAN function using some examples as done below.
Example 1 – Basic Example of TAN Function
Let us suppose we have given some angle measures in degrees as follows:-
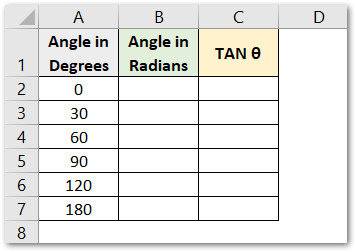
We would start by first converting the angle from degrees into radians with the use of the RADIANS Function in cell B2.
=RADIANS(A2)
Copy the following formula for all the angles to get the result in radians.
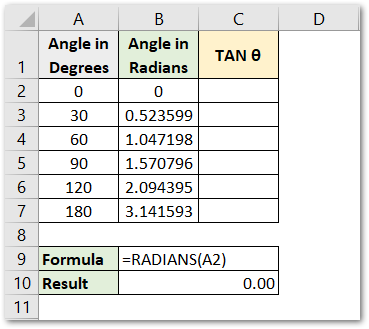
Now, we can apply the TAN formula to the result of the RADIANS Function in range B2:B7 to get the tangent value of the function. Use the following function formula in cell C2 and copy it down
=TAN(B2)
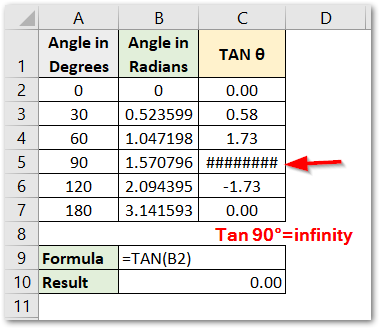
As a result, we have got the value of the Tangent function for the specified angles.
Explanation – The angle in radians is contained in column B. We have supplied the angle as the number argument of the TAN Function which gives us the required result.
The value of tangent 90 is infinity because of which we get ###### in cell C5.
Example 2 – Finding the Height of a Building from its Shadow.
Let us suppose we have a building whose shadow is formed at an angle of 50° from the sun.
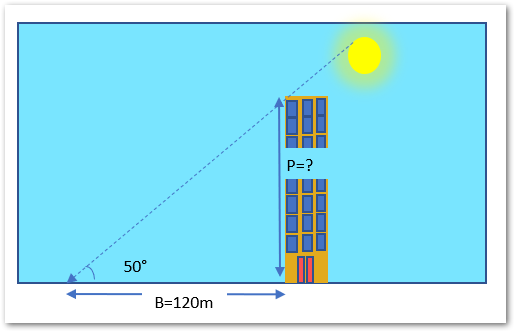
The length of the shadow is 120 m which is indicated by B=120m on the ground. We want to get the height of the building or the opposite side to the angle.
As Tan θ= P/B, therefore, P=B*Tanθ
The Height of the Perpendicular Building is given by the product of the Base ( Length of shadow ) to the Tan 50°. Use the following formula to get the height of the building.
=120*TAN(50*PI()/180)

As a result, we have got the height of the building as 143.01 meters.
Explanation – We have considered the height of the building as the P and the length of the shadow of the building to be B. The Tangent is the ratio of P and B. Therefore, the building’s height becomes the product of Tan 50° and B.
In the formula, we have multiplied the value of B=120 and tan 50°. 50 is converted into radians by multiplying with PI() / 180. The PI Function returns the constant π.
This brings us to the end of the TAN Formula blog.
Thank you for reading.
