COS Function in Excel – Usage with Examples

In the previous blog, we implemented the SIN Function. In this blog, we would now learn another important Mathematical Function, which is the COS Function in Excel. So let us begin learning.

When to Use COS Function?

The word COS represents Cosine. The COS Function calculates the value of the trigonometric ratio cosine. In a right angled triangle. Cosine refers to the ratio of the base side to the longest side.

Let us suppose we have the following right angle triangle having the base as B and hypotenuse (longest side) as H.

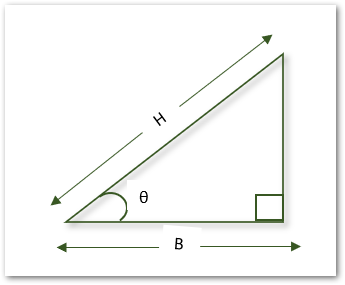
The acute angle is represented by θ. This is the angle for which we want to calculate the value of Cos θ. The value of Cos θ is given by the following ratio:-

Cos θ=B/H

Syntax and Arguments

=COS(number)

The COS function requires only one parameter to implement.

• number – This is the acute angle which we represented using the symbol θ. The most important thing to remember is that it must be in radians and not in degrees.

Converting an Angle from Degree to Radians

We can use any of the two methods to convert the angle from degree to radians.

• Using the RADIANS Function

The RADIANS Function inputs the angle in degrees and converts it into Radians. For example, we can convert 60 degrees into radians with the following formula

=RADIANS(60)

This formula returns 1.04 as in radians

• Using the PI Function

The PI() Function returns a constant value pie π. There is no input required for PI Function. We can convert an angle from degree to radians by multiplying it with  π/180.

So if we want to convert 120 degrees into radians then we can use the following formula.

=120*PI()/180

This results in an angle in radians as 2.094

Important Points to Note About COS Function

Here we have covered some important points about the COS Function of Excel so you have complete knowledge of the COS Formula.

• The number argument must be supplied in radians and not in degrees.
• The result of the COS Function always lies in the interval [-1.1]
• The COS Function came into existence in excel 2007. We cannot use COS Function in earlier versions.

Examples of COS Function in Excel

In the following section of the blog, we would learn how to implement the COS Function.

Example 1 – Basic Example of COS Function

Let us suppose we have the following angles in degrees for which we want to get the value of the Cosine Function/

We would need to convert the angle into radians so as to get the Cosine of the angles. Use the following formula in cell B2.

=COS(A2*PI()/180)

Select the range B2:B11 and press the Ctrl d key for copying the formula for the rest of the angles.

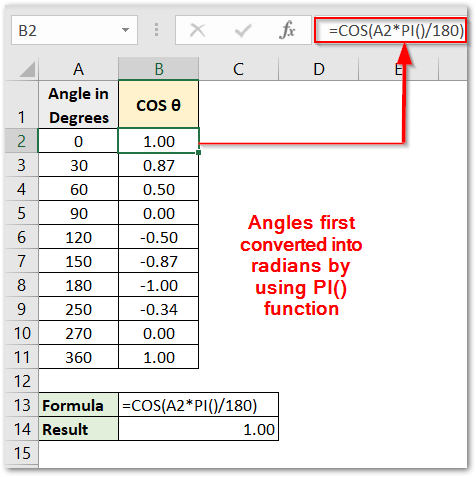
As a result, we have calculated the Cosine of angles in Excel.

Explanation – We have multiplied the angle contained in cell A2 with π / 180 with the help of the PI Function. Thereafter, the angle converted into radians is supplied as the number input of the COS Function which gives us the required result.

Here we have the graph of the Cosine function.

Example 2 – Calculating the Distance between Boat and Diver

Let us suppose we have got a Diver in the sea and the following is the illustration.

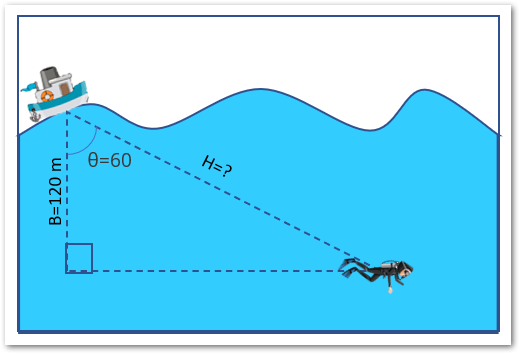
As you can see that the diver is at a depth of 120 m underwater and is at an angle of 60° from the boat. So, the side adjacent to angle θ becomes the base represented by B. We want to get the distance of the diver from the boat which is represented by H.

As Cos θ=B/H, therefore, H=B/Cos θ

Now we would use the following formula to get the distance between the boat and the diver.

=120/COS(RADIANS(60))

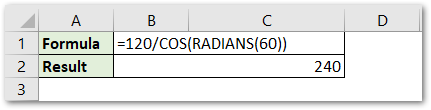
As a result, we got the distance between the boat and diver as 240 m.

This brings us to the end of COS Function blog.

Thank you for reading.