In our previous blog, we learned about the FIND function in excel which finds the position of a string. The SEARCH excel function is exactly akin to the FIND function with a small difference.
In this tutorial, we would learn how to use the SEARCH formula in excel to search for the position of a particular string or text in another text or cell.
Here we go 😎
When to Use SEARCH Function in Excel
Just like the FIND excel formula, the excel SEARCH formula is used to extract the position of a text, number, or string in a particular cell.
This function returns a numeric value which represents the position of the search term.
Unlike FIND, the SEARCH function also performs a case-insensitive search of values.
Syntax and Arguments
=SEARCH(find_text, within_text, [start_num])
The arguments of the SEARCH function are exactly same as that of FIND function and functions akin.
- find_text – In this argument, enter the text or string to find the position of.
- within_text – In this argument, enter the text or string within which you want to search the find_text.
- [start_num] – This is an optional argument. In this argument, specify the position from which the excel should start searching.
Examples of SEARCH Excel Function
Let us now learn about how does the SEARCH function work in excel with the help of some scenario based examples.
Let us first start with a basic example.
Below image shows word “Excel Unlocked”. Suppose we want to find the position of the letter ‘e’ in this string.
To achieve this, simply use the following formula:
=SEARCH(B2,A2)
OR
=SEARCH(B3,A3)
As a result, excel would return a numeric value 1. This means that the letter ‘e’ or ‘E’ is at position 1 in word “Excel Unlocked”.
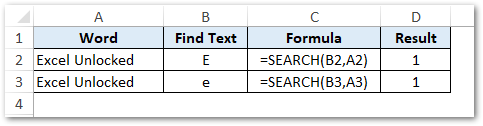
Explanation – From the above example, you would notice that the SEARCH function does not discriminate between upper case ‘E’ and lower case ‘e’. This means that, unlike the FIND function, the SEARCH formula performs a case-insensitive search of values.
By default, the SEARCH function returns the position of the first occurrence of the find_text (unless you specify the [start_num] argument value)

Let us now learn the purpose of and how to use the [start_num] argument in SEARCH function.
The [start_num] determines from which position should the excel start finding the find_text.
In the word “Excel Unlocked”, there are two ‘L’s. To find the position of the second letter in the word, use the following formula:
=SEARCH(B2,A2,6)

As a result, excel returns the output position as 9.
Do Not Miss These Points
- The SEARCH function performs a case-insensitive search of the sting. That means it does not discriminate between upper case and lower case search. For the case-sensitive search of string, use the FIND excel function.
- The SEARCH function will return the excel error code #VALUE,
- if it does not find the find_text in the within_text or
- when [start_num] value is more than within_text length.

- When there are multiple occurrences of the find_text, the SEARCH function will return the position of the first occurrence, by default (unless you specify [start_num]) – covered above.
Thank You 🙂
